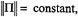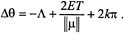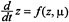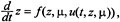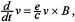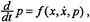This article explores how SiC cascodes perform in difficult conditions—including avalanche mode and divergent oscillations—and looks at their performance in circuits that utilize zero voltage switching.
Silicon Carbide (SiC) cascodes have an edge with major characteristics like normalized ON-resistance to chip area (RDSA), device capacitances, and ease of gate drive. However, designers are a cautious lot and understand that headlines are not always the full story. We are naturally wary of changing away from technologies that have proven to be robust over decades, as with IGBTs for example, but what these devices do under real dynamic conditions of voltage stress and external faults is an area of particular concern.
Out-Running the Avalanche
The beauty of a cascode is the use of a low voltage Si-MOSFET which, in conjunction with a normally-ON SiC JFET, gives the device its overall low ON-resistance, fast body diode, and easy gate drive (Figure 1).

Figure 1. SiC cascode
Some might worry that dynamically, the MOSFET could see high drain voltages and enter avalanche mode in normal operation when driven OFF. Could this result in extra losses or even device failure? In cascodes formed with lateral-construction GaN HEMT cells, this is a real possibility as the finite drain-source capacitance CDS of the GaN device forms a ‘pot-down’ with the CDS of the Si-MOSFET and can dynamically leave a high voltage on the MOSFET drain (Figure 2). The SiC JFETs in SiC cascodes are different though, with their vertical ‘trench’ construction, the SiC-JFET CDS value is vanishingly small so that the Si-MOSFET never practically sees the high voltage from the pot-down effect.

Figure 2. Cascode arrangement of Si MOSFET and GaN HEMT cell with voltage dynamically ‘potted-down’ leaving a high voltage on the Si-MOSFET drain
Embracing the Avalanche
There are occasions though when avalanche is desirable, protecting the device from transients produced by inductive loads. GaN cascodes have no avalanche rating and will simply fail with overvoltage whereas the gate-drain diode of the SiC cascode JFET breaks over, passing current through RG, dropping voltage to turn the JFET ON. The Si-MOSFET does now avalanche, but in a controlled way if avalanche diodes are built into each cell. To allay any worries that this intentional avalanche effect is possibly damaging, manufacturers like UnitedSiC prove the point with parts qualified to 1000 hours of operation biased into avalanche at 150°C. As an additional confidence measure, all UnitedSiC parts are subjected to 100% avalanche at final test.
SiC Cascodes Maintain Zero Voltage Switching
Another situation in which the low CDS of the SiC-cascode scores is in circuits that utilize zero voltage switching (ZVS); a power switch is only allowed to change state when the load voltage has resonantly swung down to zero volts, giving a lossless transition (Figure 3).

Figure 3. Transition as voltage rings down gives zero voltage switching
If the CDS value of the high voltage switch in a cascode is high, there is a danger that induced current through it can discharge its gate-source capacitance along with the Si-MOSFET drain-source capacitance, turning the high voltage switch prematurely ON before the drain voltage has swung to zero. In this case, ZVS is lost and power is dissipated. The absence of CDS in the SiC-Cascode JFET means that the effect cannot happen.
Divergent Oscillations
A similar effect called divergent oscillation was identified when cascodes were first assembled with discrete devices for the high and low voltage switches. The different technology devices in separate packages and from typically different manufacturers had naturally high stray capacitances and connection inductances which had their own tolerances as well.
Work by X. Huang, Fred Lee and others [1] showed that on turn-off at high currents, a finite value of CDS for the high voltage switch could resonate with package inductance causing current injection into the cascode mid-point. The current could partially turn on the high voltage switch reducing the effective resonance capacitance which increases the circuit characteristic impedance. This has the effect of increasing the amplitude of the resonant swing.
The result was a runaway or ‘divergent’ oscillation that could cause dissipation and device failure (Figure 4). The paper suggested that a dissipative RC snubber at the midpoint was a solution but actually found that just a capacitor was effective. This had to be several nano-farads though and did cause some extra losses particularly at high frequencies. SiC cascodes with near-zero CDS avoid the issue completely and co-packaging of the high and low voltage switches reduces package inductance to a low value as well allowing the full high-frequency capability of the cascode to be exploited.
Figure 4. Divergent oscillations (source: see Reference 1)
SiC Cascodes are Robust
SiC cascodes perform at their best when the Si-MOSFET is custom-designed for the application and co-packaged with the JFET. When implemented this way, the MOSFET does not see voltage stress and provides a fast body diode. The JFET effectively dominates the device characteristics for ON-resistance, and voltage withstand while the combination gives a level of robustness against unintended avalanche and the various loss-inducing effects of high CDS values seen with other technologies such as superjunction MOSFETs and GaN HEMT cells.
References
[1] X. Huang, W. Du, F.C. Lee, Q. Li and Z. Liu, “Avoiding Divergent Oscillation of a Cascode GaN Device Under High-Current Turn-Off Condition”, IEEE Trans. Power Electronics, 2017




















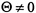
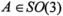
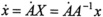 . Since
. Since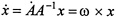 , which defines the spatial angular velocity vector ω .The corresponding body angular velocity is defined by Ω; =
, which defines the spatial angular velocity vector ω .The corresponding body angular velocity is defined by Ω; =
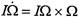 . The body angular momentum is defined, analogous to linear momentum
. The body angular momentum is defined, analogous to linear momentum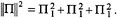 . This follows from conservation of π and the fact that
. This follows from conservation of π and the fact that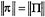
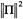 .
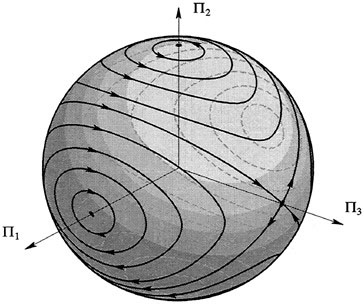
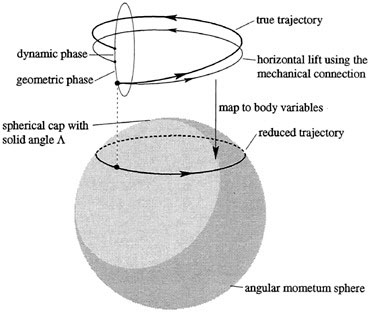
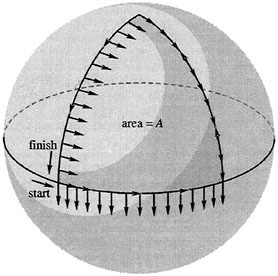
.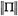 , the evolution in time of any initial point Π(0) is constrained to the sphere
, the evolution in time of any initial point Π(0) is constrained to the sphere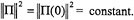 . Thus we may view the Euler equations as describing a two-dimensional dynamical system on an invariant sphere. This sphere is called the
. Thus we may view the Euler equations as describing a two-dimensional dynamical system on an invariant sphere. This sphere is called the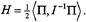 . Since solutions curves are confined to the sets where
. Since solutions curves are confined to the sets where